GSW
Introduction
Ce cryptosystème symétrique qui est "somewhat" homomorphe, repose sur des notions simples et a une sécurité qui repose sur un problème qui échappe pour l'instant aux algorithmes quantiques.
Tout d'abord, on remarque la chose intéressante suivante :
Soient \(C_1\) et \(C_2\),deux matrices carrées de taille \(n\), et \(s\) un de leur vecteur propre, de valeur propre respective \(m_1\) et \(m_2\). On a alors : $$s*C_1 = s*m_1,$$ $$s*C_2 = s*m_2,$$ $$s*(C_1*C_2) = s*(m_1*m_2),$$ $$s*(C_1+C_2) = s*(m_1+m_2)$$ On a donc une ébauche de ce à quoi pourrait ressembler notre cryptosystème : \(s\) serait notre clé secrète, \(C\) serait notre chiffré et \(m\) notre message. Et on aurait la relation : $$s*C = s*m$$ Pour chiffrer il faudrait trouver une matrice \(C\) ayant un vecteur propre \(s\) et une valeur propre correspondante \(m\). Et pour déchiffrer, il suffirait de multiplier la matrice \(C\) par \(s\) pour obtenir un vecteur \(s*m\). Il ne resterait plus alors qu'à obtenir la norme de ce vecteur et la diviser par la norme de \(s\) pour obtenir \(m\).
Apparait alors le problème suivant : ce cryptosystème n'est pas sécurisé. Il est en effet bien trop aisé de trouver \(m\) et \(s\) à partir de \(C\). Pour régler ce problème, on ajoute du bruit : on a alors des valeurs propres et un vecteur propre approximés : \begin{equation} s*C = s*m + e \end{equation} On a ici ajouté un bruit, qui correspond à un vecteur e. Regardons à présent comment évolue ce bruit lorsque l'on effectue des opérations : On a \(s*C_1 = s*m_1 + e_1\) et \(s*C_2 = s*m_2 + e_2\), d'où : $$s*(C_1+C_2) = s*(m_1 + m_2) + (e_1 + e_2)$$ $$s*(C_1*C_2) = (s*C_1)*C_2$$ $$= (s*m_1 + e_1) * C_2$$ $$= s*m_1*C_2 + e_1*C_2$$ $$= m_1*(s*C_2) + e_1*C_2$$ $$= m_1*(s*m_2 + e_2) + e_1*C_2$$ $$= s*(m_1*m_2) + m_1*e_2 + e_1*C_2$$ On peut donc remarquer que le bruit augmente pour chaque opération : $$e_{add} = e_1 + e_2$$ $$e_{mult} = m_2*e_2 + e_1*C_2$$ Nous verrons par la suite quelles sont les implications de cette augmentation du bruit et comment faire en sorte que le bruit augmente plus faiblement. Mais tout d'abord, essayons de construire un cryptosystème sécurisé.
Sécurité et problème LWE
Montrer qu'un cryptosystème est sécurisé consiste à montrer que casser ce cryptosystème reviendrait à résoudre un problème difficile. Nous allons donc découvrir dans un premier temps le problème LWE (Learning With Errors) puis nous allons voir comment le cryptosystème du vecteur propre approximé est concrètement construit à l'aide de ce problème.
Le problème LWE
Le problème LWE (Learning With Errors) a été introduit par Oded Regev en 2005. Ce problème consiste à retrouver un vecteur secret \(s\in\mathbb{Z}^n_q\) à partir d'une séquence d'équations linéaires aléatoires et "approximées" sur \(s\). Par exemple, ladite séquence pourrait être : $$14s_1+15s_2+5s_3+2s_4\approx8\ (mod \ 17)$$ $$13s_1+14s_2+14s_3+6s_4\approx16\ (mod \ 17)$$ $$6s_1+10s_2+13s_3+1s_4\approx3\ (mod \ 17)$$ $$10s_1+4s_2+12s_3+16s_4\approx12\ (mod \ 17)$$ $$9s_1+5s_2+9s_3+6s_4\approx9\ (mod \ 17)$$ $$3s_1+6s_2+4s_3+5s_4\approx16\ (mod \ 17)$$ $$\vdots$$ $$6s_1+7s_2+16s_3+2s_4\approx3\ (mod \ 17)$$ Dans cet exemple, \(s\in\mathbb{Z}^4_{17}\). Le \(\approx\) signifie que chaque équation est vraie à une erreur près. C'est-à-dire qu'à chaque équation, on pourrait ajouter un terme compris entre \(erreur\) et \(-erreur\) pour que les \(\approx\) deviennent des égalités. Si cette erreur est égale à 0, alors les \(\approx\) peuvent être remplacées par des \(=\) et il est aisé de retrouver \(s\) à partir des équations, en effectuant une élimination de Gauss. Si l'erreur est faible (\(\pm1\) par exemple) il est encore possible de retrouver \(s\). Mais plus l'erreur augmente et plus le problème est difficile. Lorsque l'erreur est maximale (lorsqu'elle vaut \(q\)) alors il est impossible de retrouver \(s\) car il est impossible de le distinguer de l'erreur. Dans la séquence de l'exemple, l'erreur était de \(\pm1\), et \(s\) valait \((0,13,9,11)\). Reformulons le problème ainsi : Soient les paramètres \(n\geq1\) (la taille), \(q\geq2\) (le modulo) et \(\alpha\in[0,1]\) (la difficulté). Soit un vecteur secret \(s\in\mathbb{Z}^n_q\). On a en entrée un certain nombre d'équations : $$a_{11}*s_1 + \ldots + a_{1n}*s_n + e_1 = b_1 \ (mod \ q)$$ $$a_{21}*s_1 + \ldots + a_{2n}*s_n + e_2 = b_2 \ (mod \ q)$$ $$\vdots$$ $$a_{k1}*s_1 + \ldots + a_{kn}*s_n + e_k = b_k \ (mod \ q)$$ Où les \(a_{ij}\) et les \(b_i\) sont connus, les \(a_{ij}\) sont répartis uniformément et les \(e_i\) sont choisis aléatoirement parmi \(]-\alpha q, \alpha q[\). Retrouver \(s\) est un problème difficile pour certaines valeurs de \(\alpha\).
Construire un cryptosystème à partir de LWE
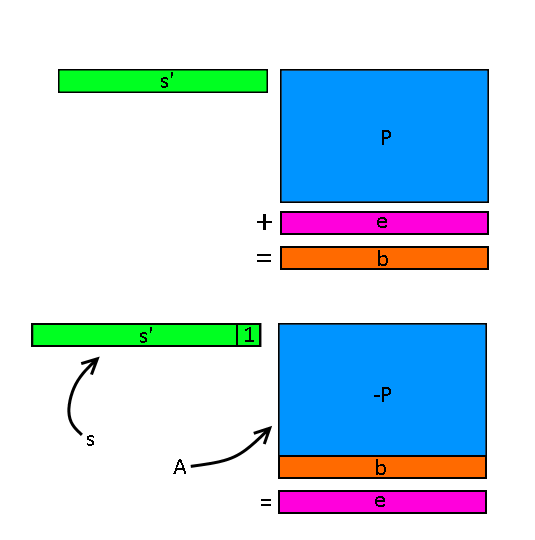
On pose \(P\), une matrice uniforme dans \(\mathbb{Z}^{n*M}_q\).
On pose un vecteur bruit \(e\) tel que \(|e_i|\leq|\alpha q|\)
et un vecteur secret \(s'\in\mathbb{Z}^n_q\). On pose \(b = s'P + e\).
Si les paramètres \(n,q\) \(et\) \(\alpha\) ont été bien choisis alors
il n'est pas possible de retrouver \(e\) ni \(s'\) à partir de \(P\) et \(b\)
(cela reviendrait à résoudre le problème LWE efficacement).
Maintenant, on pose la matrice \(A\) qui correspond à la matrice \(-P\)
à laquelle on aurait ajouté une ligne \(b\) à la fin. On remarque alors
que \(sA=e\) où \(s\) est le vecteur \(s'\) auquel on ajoute une case à
la fin avec la valeur 1.
On remarque que retrouver \(s\) ou \(e\) à partir de \(A\) revient à
résoudre le LWE problème, ce qui n'est en pratique pas faisable.
Voyons comment exploiter cela pour faire un cryptosystème.
On garde les éléments précédents, où \(A\) sera notre clé publique et \(s'\) notre clé privée. Soit notre message \(y\in\mathbb{Z}^n_q\), un vecteur colonne. On pose \(C_y\) le chiffré correspondant tel que : $$C_y = Ar + y$$ Où \(r\) est un vecteur colonne à \(M\) éléments qui valent chacun \(0\) ou \(1\). On précise également que les \(0\) et les \(1\) sont répartis uniformément dans le vecteur \(r\). Alice envoie ce message à Bob, qui va le déchiffrer avec sa clé secrète \(s\) en utilisant la relation suivante : $$s*C_y = s(Ar + y) = s*A*r + s*y$$ $$= e*r + s*y$$ Etant donné que les éléments de \(r\) ont des petites valeurs et que Bob connait \(e\), il est possible de débruiter le résultat, et de ne garder que \(s*y\), et donc d'obtenir finalement \(y\). Précisons que le vecteur \(r\) permet au système d'être non déterministe, c'est-à-dire qu'un même message n'aura pas toujours le même chiffré. Précisons également que retrouver \(y\) à partir de \(C_y\) et \(A\) revient à retrouver le bruit \(e\) à partir de \(A\), autrement dit à résoudre efficacement le problème LWE.
Le cryptosystème obtenu peut se généraliser aux matrices : on utilise maintenant une matrice \(R \in \mathbb{Z}^{M*N}_q\) à la place de \(r\) et une matrice \(Y \in \mathbb{Z}^{(n+1)*N}_q\) à la place de \(y\). On conserves les égalités obtenues précédemment :
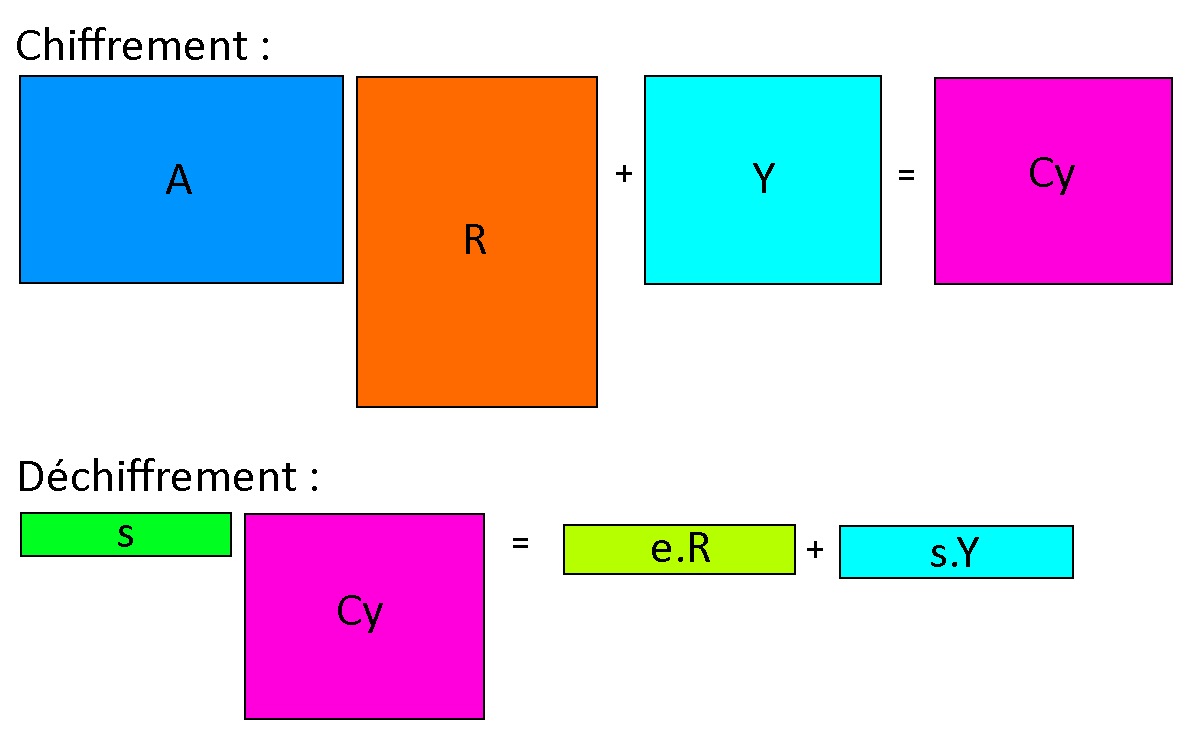
On retrouve la relation décrite précédemment : \(s*C_y = s*y + e'\), où \(e' = e*R\). On sait donc que le bruit va augmenter au fil des opérations, de la façon suivante : $$e'_{add} = e'_1 + e'_2$$ $$e'_{mult} = y_2*e'_2 + e'_1*C_2$$ Pour éviter que le bruit s'accroisse trop rapidement, il faut donc modifier notre cryptosystème.
Cryptosystème final
Décomposition binaire et matrice Gadget
Pour réduire les valeurs de \(C\), nous allons créer la matrice qui correspond à sa décomposition binaire. Soit la fonction \(bits\) qui prend en entrée une matrice et qui retourne la matrice correspondant à sa décomposition binaire. Par exemple : $$ C= \begin{pmatrix} 3 & 2 \\ 1 & 0 \end{pmatrix} $$ $$ bits(C) = \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ 0 & 0 \\ 1 & 0 \end{pmatrix} $$ Considérons à présent la matrice suivante : $$ G = \begin{pmatrix} 2 & 1 & 0 & 0 \\ 0 & 0 & 2 & 1 \end{pmatrix} $$ On remarque que \(G*bits(C) = C\). Cette matrice qui permet d'effectuer l'opération inverse de la décomposition binaire est appelée matrice Gadget. Pour se simplifier la vie, on notera donc \(bits(C) = G^{-1}(C)\) pour la suite. Voyons à présent comment se présente notre cryptosystème final.
Cryptosystème final
On se remémore le cryptosystème décrit précédemment, et on garde notre clé publique \(A\) et notre clé privée \(s\). A partir de maintenant, pour des raisons de lisibilité, on nommera \(e\) le bruit d'un message chiffré, c'est-à-dire le bruit que l'on nommait \(e'\) auparavant. On pose notre fonction de chiffrement (Enc, comme "Encryption", qui se traduit par "Chiffrement") : $$C = Enc(m,R) = AR + mG$$ Remarquons qu'elle ressemble à celle qui était décrite précédemment, excepté que \(y\) est exprimé comme \(m*G\) où \(m\) est notre message et \(G\) est la matrice Gadget. On précise également que \(m \in \{0,1\}\), autrement dit tous les messages sont des bits et le cryptosystème utilise des circuits logiques. On pose notre fonction de déchiffrement (Dec, comme "Decryption", qui se traduit par "Déchiffrement") : $$Dec(C) = s*C*G^{-1}(\frac{q}{2}u)$$ Où \(u\) est un vecteur colonne de la même taille que \(s\) dont tous les éléments valent \(0\) sauf le dernier qui vaut \(1\). Analysons cette fonction de déchiffrement : $$s*C*G^{-1}(\frac{q}{2}u) = s*(AR + mG)*G^{-1}(\frac{q}{2}u)$$ $$= s*A*R*G^{-1}(\frac{q}{2}u) + s*m*G*G^{-1}(\frac{q}{2}u)$$ $$= e*G^{-1}(\frac{q}{2}u) + m*s*G*G^{-1}(\frac{q}{2}u)$$ $$= e*G^{-1}(\frac{q}{2}u) + m*s*\frac{q}{2}u$$ $$= e*G^{-1}(\frac{q}{2}u) + \frac{q}{2}*m*s*u$$ On rappelle maintenant que \(s\) est un vecteur ligne dont le dernier élement vaut \(1\) et que \(u\) est un vecteur colonne dont tous les éléments valent \(0\) sauf le dernier qui vaut \(1\). On en déduit donc que \(s*u = 1\). D'où : $$Dec(C) = e*G^{-1}(\frac{q}{2}u) + \frac{q}{2}*m$$ Le bruit est faible, car \(G^{-1}(\frac{q}{2}u)\) ne contient que des \(0\) et des \(1\). Le message \(m\) est soit égal à \(1\), soit égal à \(0\), donc pour débruiter, il suffit de voir si le résultat de la fonction de déchiffrement est supérieur à \(\frac{q}{2}\). Si c'est le cas, on en déduit \(m=1\), sinon \(m=0\). On comprend également mieux pourquoi l'augmentation du bruit finit par empêcher le déchiffrement : au delà d'un certain seuil de bruit, la fonction de déchiffrement ne pourra retourner que des résultats supérieurs à \(\frac{q}{2}\).
Opérations : multiplication et porte NAND
Rappelons la relation suivante : $$s*C = e + m*s*G$$ La multiplication de deux chiffrés \(C_1\) et \(C_2\) s'obtient ainsi : $$C_{mult} = C_1*G^{-1}(C_2)$$ Cherchons à déterminer l'accroissement du bruit : $$s*C_1*G^{-1}(C_2) = (e_1 + m_1*s*G)*G^{-1}(C_2)$$ $$= (e_1 * G^{-1}(C_2)) + m_1*s*G*G^{-1}(C_2)$$ $$= (e_1 * G^{-1}(C_2)) + m_1*s*C_2$$ $$= (e_1 * G^{-1}(C_2)) + m_1*(e_2+m_2*s*G)$$ $$= (e_1 * G^{-1}(C_2)) + (m_1 * e_2) + (m_1*m_2*s*G)$$ On pose \(e_{mult} = (e_1 * G^{-1}(C_2)) + (m_1 * e_2))\). On a bien \(s*C_{mult} = e_{mult} + m_1*m_2*s*G\). Rappelons que les messages \(m1\) et \(m2\) représentent des bits, sur lesquels on cherche à effectuer des opérations logiques. On pose : $$C_{nand} = G - C_{mult}$$ D'où : $$Dec(C_{nand}) = Dec(G-C_{mult})$$ $$=s*(G-C_{mult})*G^{-1}(\frac{q}{2}u)$$ $$=s*G*G^{-1}(\frac{q}{2}u) - Dec(C_{mult})$$ $$=1 - Dec(C_{mult})$$ Etant donné que \(m1\) et \(m2\) sont égaux à \(0\) ou \(1\), \(Dec(C_{mult})\) correspond au ET logique entre \(m1\) et \(m2\). Par conséquent \(Dec(C_{nand})\) correspond au NON-ET logique. On a ainsi défini comment réaliser la porte logique NON-ET (NAND en anglais) et on a déterminé que le bruit résultant de cette opération était \(e_{nand} = e_{mult}\). Cette opération a l'avantage d'être universelle, c'est-à-dire qu'il est possible de réaliser n'importe quelle fonction logique sous la forme d'un circuit de portes NAND.
Augmentation du bruit et profondeur maximal d'un circuit
Petit rappel : \(N\) est le nombre de colonnes de \(Y\), la matrice qui représente le message. Concrètement, la matrice qui représente le message est \(m*G\) où \(m\) est ledit message et \(G\) la matrice Gadget. On en déduit que \(N\) est le nombre de lignes des matrices \(G^{-1}\). Etant donné que les matrices \(G^{-1}\) ne contiennent que des \(0\) et des \(1\), on peut en déduire que quelque soit le vecteur ligne \(v\) : \(||v*G^{-1}|| \leq ||v|| * N\).
On rappel également que \(e_{nand} = e_{mult} = (e_1 * G^{-1}(C_2)) + (m_1 * e_2))\). On a par conséquent :
$$||e_{nand}|| \leq ||e_1|| * N + ||e_2|| * m_1$$
En rappelant que nos messages ne sont que des \(1\) ou des \(0\), on a :
$$||e_{nand}|| \leq ||e_1|| * N + ||e_2|| * m_1 \leq (N+1)*max(||e_1||,||e_2||)$$
Considérons maintenant le circuit suivant :
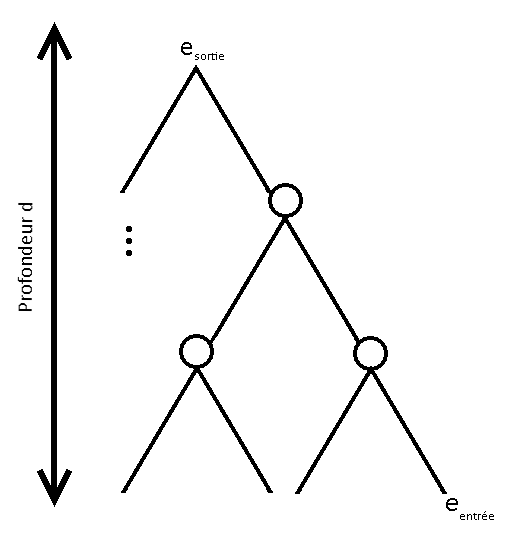Ce circuit étant constitué de portes NAND, on a la relation suivante, où \(e_i\) est le bruit maximum à l'étape \(i\) :
$$||e_{i+1}|| = (N+1)*||e_i||$$
Le circuit ayant une profondeur \(d\), on en déduit que :
$$||e_{sortie}|| \leq (N+1)^d*||e_{entrée}||$$
On rappelle que le bruit \(e_{entrée}\) est le produit entre une matrice \(R\) (ne contenant que des \(1\) et des \(0\)) et un vecteur ligne à \(M\) colonnes et où chaque élément est inférieur en valeur absolu à \(\alpha q\). Ainsi \(||e_{entrée}|| \leq M\alpha q\).
Enfin, on arrive à la conclusion que \(||e_{sortie}|| \leq (N+1)^d*M\alpha q\).
Pour que le message puisse être débruité, on rappelle que le bruit doit être très inférieur en norme à \(q\). Par conséquent, ce cryptosystème est limité en nombre d'opérations par la taille de la clé \(q\).
Pour découvrir des cyptosystèmes qui ne sont pas limités en nombre d'opérations,
vous pouvez vous référer à la section Bootstrapping.